Las proporciones del rostro de la Gioconda hecho con rectángulos áureos.
El número áureo o Phi es un número irracional. Phi (Φ = 1.6180339887498948…) pronunciado “fi”, al igual de pi (p = 3.1415926535897932…) su representación decimal no tiene periodo. Mientras π es fruto de la relación entre una circunferencia y su diámetro, Φ es fruto de la relación entre dos segmentos de una recta. Donde la relación entre estos segmentos es la siguiente: en una recta hay dos segmentos a y b, a es más grande que b. El segmento a tiene la misma relación con la recta entera que el segmento b con el segmento a. Aquí puedes ver una representación gráfica:
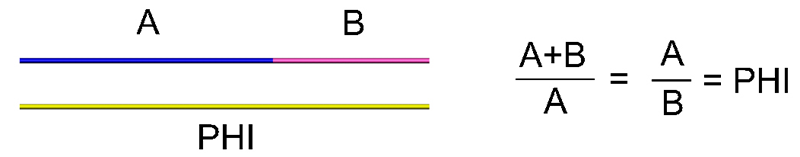
Puedes comprobar la formula aplicando el valor de Phi a A+B, donde A es igual a 1 y B es el recíproco de Phi: 0.6180339887498948…
Curiosamente el recíproco de Phi tiene los mismos decimales que Phi. Con estos datos un rectángulo áureo es en el que sus lados tienen como relación Phi. En el siguiente gráfico puedes ver como trazar fácilmente un rectángulo áureo:
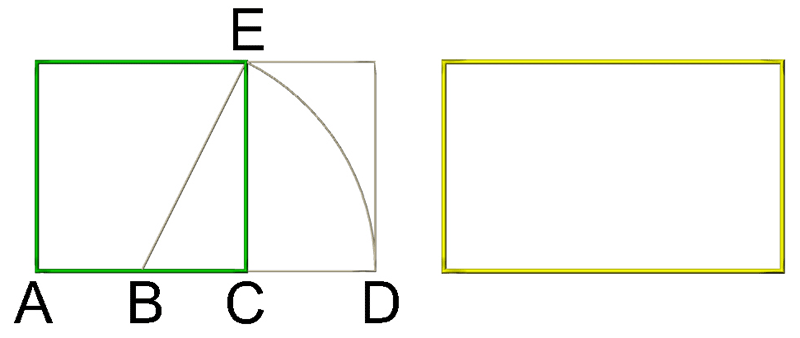
Primero trazamos un cuadrado, después trazamos un arco que tiene por centro B, empieza en E y termina en D. B es el centro del la base del cuadrado, E su esquina superior derecha y D es donde se interseca el arco con la prolongación recta de la base del triangulo. En amarrillo el rectángulo áureo que acabamos de trazar.
Esta proporción áurea se puede encontrar en los animales, plantas, sistema solar... Y también en el arte, como te voy a explicar a continuación.
La construcción del "mapa" del rostro de la Gioconda pintada por Leonardo da Vinci es similar a la construcción de la espiral áurea del nautilo.
El rostro de la Mona Lisa enmarcado en rectángulos áureos:

La construcción fase por fase del mapa áureo del rostro de Mona Lisa

1- En el esquema nº 1 puedes ver como el rostro de la Gioconda se encuadra perfectamente en un rectángulo áureo.
2- Dentro de ese rectángulo áureo dibujo un cuadrado en el esquema nº 2 quedando arriba otro rectángulo áureo.
3- En el rectángulo áureo obtenido en el esquema nº 2 realizo la misma operación (nº 3).
4- Vuelvo a realizar la misma operación en el esquema nº 4.
5- En el nº 5 traslado simétricamente según la línea que pasa justo encima de los ojos el cuadrado grande de arriba y el último rectángulo áureo obtenido. Puedes ver que la línea que apunto sale exactamente del nacimiento del pelo (justo en la raya del pelo) pasa por la mitad de la nariz y termina en la mitad de donde empieza la boca de Mona Lisa.
6- En el dibujo nº 6 realizo la misma operación descrita en el nº 2 dos veces. El punto que señalo es exactamente el centro de la pupila del ojo izquierdo de la Gioconda y en el nº 8 el ojo derecho.
7- En el siguiente dibujo (nº7) traslado simétricamente según la línea que va del pelo a la boca lo dibujado en el nº 6.
8- En el nº 8 trazo un nuevo rectángulo áureo en el cual la esquina inferior izquierda del último cuadrado dibujado es exactamente el centro de la pupila del ojo derecho de la Gioconda.
Había leído en la red que el rostro de la Gioconda de Leonardo da Vinci se encuadra en un rectángulo áureo, pero yo he ido un poco más allá.
Mi teoría está publicada en Wikipedia desde el 24 diciembre de 2006. Nadie antes había pensado en esto... Después muchos me han copiado y entre ellos muchos sin hacer ninguna mención al autor.
Mi teoría sobre la Gioconda fue seleccionada como imagen del mes en Mathematics Portal de noviembre de 2007.
Esta mítica obra de Leonardo da Vinci se encuentra en el museo del Louvre en Paris.
Ir al sitio oficial del museo del Louvre 
El arte y las matemáticas forman parte de mis pasiones, como crear tallas en madera. Las realizo por encargo, totalmente personalizadas. Aquí tienes un ejemplo:

Pida un presupuesto para su talla en madera sin compromiso.
Trabajos hechos en España por Tallas en madera Castor
© 2005-2025 Castor.es - Tallas en madera castor - Calle Málaga, 21 - 11190 Benalup-Casas Viejas - España

